
さぁ、今日も週末のテストに向けて
計画通り学習していこう!
………おや………?
左の手前3人組はどうしたのでしょう。
手元を見ると、円周角の定理を使った
ある問題に悩まされていました。
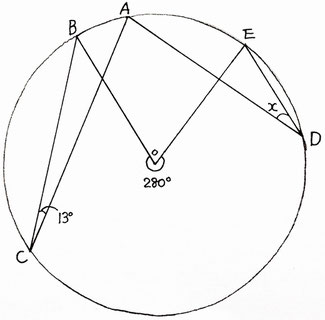
⇦それがこちら。
∠xの大きさを求める問題です。
これより以前の問題は解けていたのに、
ちょっと見た目が変わる途端
それまでの解き方から外れて、違う切り口で
考えている様子。
ではどのように解いているのか
三人の考え方を見てみましょう。
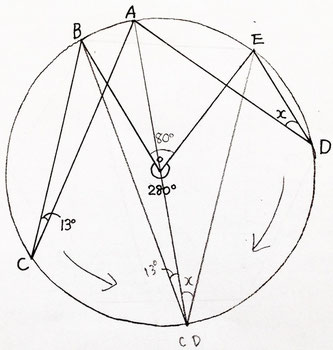
こちらの生徒さんは、今わかっている中心角の280°を360°から引いて、残りの角度を出しています。
それからBとEを直線で結び、二等辺三角形を作っていますね。二等辺三角形の底角は等しいことから、∠OBEと∠OEBがそれぞれ50°であることを出したところで手が止まり…。
求めたい∠x周辺の角度を何とかして出したかったようです。
こちらの生徒さんは、途中までは左隣の生徒さんと同じ考え方です。
異なるのは、線分BOと線分EOをそれぞれ円周までのばし直径を書いて、直角三角形を作っているところです。
90°の角度を作った意図は、左の際とさんと同じく、∠x周辺の角度を出すためだったそうです。
こちらの生徒さんも、∠x周辺の角度を出そうとしました。
そこで利用したのが正六角形。
コンパスを使って作図をしたような跡はなく、どのようにして正六角形を書いたのかは不明です。定規を使って執念で書いたのでしょうか。
しかし、正六角形の角度を活かすことができず迷走…。
三人が三人揃って全く別の発想で考えていく姿勢がたまらないですね。
このままそれぞれの考えを深めてもらおうとしばらく見守っておりましたが、結局どうにも答えに辿り着けないようで、助けを求めに来ました。
自ら新たな発想で切り開いていく姿勢はとても素敵です。しかし、習ったことも活用していくのですよ!
ということで、AOを結んだ線分を円周まで延長させ直径を作り、BとEをそれぞれ結びましょう。
…と、ここまで解説したところで
「あぁ~、なんだ…めっちゃ簡単にできるじゃん…」
と悔しがる3人組。
それに気づくことも学習の一つです。
良い時間を過ごしましたね。

その後、解き方を理解した生徒たちは、
前の自分たちと同じく苦戦をしている仲間に
助言をするのでした。




コメントをお書きください